Теория по теме "Производная. "
Рассмотрим функцию y = f (x), определенную на некотором промежутке. Пусть x0 — фиксированная точка из области определения этой функции, x — произвольная точка из некоторой окрестности точки x0, причем x ≠ x0.
Разность x − x0 называется приращением аргумента в точке x0.
Разность f (x) − f (x0) называется приращением функции в точке x0.
Приращение аргумента в точке x0 обозначается Δx (читается «дельта икс»), приращение функции в точке x0 обозначается Δy (читается «дельта игрек») или Δf (читается «дельта эф»). Таким образом,
Δx = x − x0, откуда x = x0 + Δx;
Δy = Δf = f (x) − f (x0) = f (x0 + Δx) − f (x0).
Используя определение производной можно получить


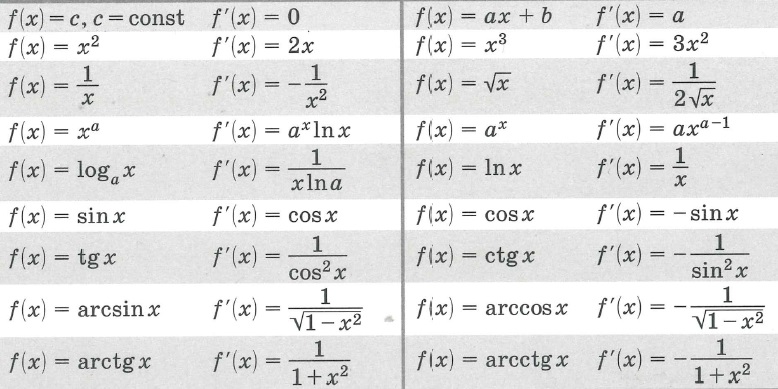



Комментариев нет:
Отправить комментарий